卡尔达诺的《论代数法则》的简单介绍
1、代数基本定理是数学中基础且重要的一环,它断言任何复系数多项式方程在复数域中至少有一个根这一定理有多种等价表述,其中一个表示是任意复系数多项式在复数域上必定存在一个一次因式代数基本定理的演变始于17世纪,当时讨论方程根的数量问题吉罗拉莫·卡尔达诺是首个意识到三次方程可能有三个根;作为赌徒,卡尔达诺写了一篇论掷骰子游戏,他采用数学概率学对掷骰子的赢面进行了换算,而作为一个占星学家,他得到了教皇皮乌斯五世的赏识,教皇支付给他终身年薪,让他待在皇宫,专心研究的他的占星学卡尔达诺出生于1501年,他的父亲是一个律师,跟知名画家达芬奇是好友,卡尔达诺在达芬奇的影响下。
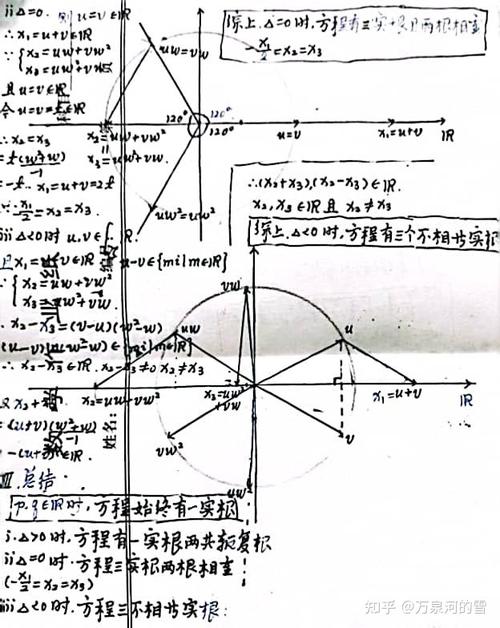
2、卡尔达诺最重要的数学著作是1545年在纽伦堡出版的大术Ars magna全名为大术,或论代数法则Artis magnae,sive de regulis algebraicis liber unus该书系统给出代数学中的许多新概念和新方法例如三四次代数方程的一般解法确认高于一次的代数方程多于一个根已知方程的一个根将;他在数学上的成就尤为突出,1545年的大术一书中,他首次发表了三次代数方程的一般解法,即著名的卡尔达诺公式,尽管这一方法的思路源于塔塔利亚,导致了两人多年的争议书中还记录了由学生费拉里发现的四次代数方程的解法,并引入了复数的概念卡尔达诺在概率论领域的贡献同样重要,他死后出版的论;打开的概率为815利用排列组合的知识求解,具体过程如下开门的概率=1不能开门的概率 不能开们的概率也就是两次都没抽到钥匙的事件发生的概率 两次都没抽到钥匙的事件发生的概率=两次都没有抽到钥匙的情况抽到钥匙的所有情况 两次都没有抽到钥匙的情况=C7 2=21 抽到所有钥匙的情形为=C10 2;邦贝利在他的著作中阐述了三次方程不可约的情形,并使用了虚数,还改进了当时流行的代数符号符号代数学是由16世纪的法国数学家韦达确立的他于1591年出版了分析方法入门,对代数学加以系统的整理,第一次自觉地使用字母来表示未知数和已知数韦达在他的另一部著作论方程的识别与订正中,改进了三四次方程的。
3、约公元1360年 法国N奥尔斯姆撰比例算法,引入分指数概念,又在论图线等著作中研究变化与变化率,创图线原理,即用经纬度相当于横纵坐标表示点的位置并进而讨论 函数图像 公元1427年 阿拉伯卡西著算术之钥,系统论述算术代数的原理方法,并在圆周论中求出圆周率17位;高等代数不是高等数学 ,两者区别如下一指代不同 1高等代数代数在讨论任意多个未知数的一次方程组,也叫线性方程组的同时还研究次数更高的一元方程组2高等数学 是由微积分学,较深入的代数学几何学以及它们之间的交叉内容所形成的一门基础学科二特性不同 1高等代数高等代数是;三次方程的一般形式可以表示为ax3 + bx2 + cx + d = 0为了使用卡尔达诺公式,通常需要通过特定的代换将原方程化简为一个更易于处理的形式求解步骤将三次方程化简为特定形式后,可以直接套用卡尔达诺公式来求解卡尔达诺公式提供了三个解,这些解是通过一系列复杂的代数操作得到的,包括求立方根;回答代数在1545年出版的大术一书中,他第一个发表了三次代数方程一般解法的卡尔达诺公式,也称卡尔丹诺公式解法的思路来自塔塔利亚,两人因此结怨,争论经年书中还记载了四次代数方程的一般解法由他的学生费拉里发现此外,卡尔达诺还最早使用了复数的概念概率论卡尔达诺死后发表的论赌博游戏;还改进了当时流行的代数符号符号代数学是由16世纪的法国数学家韦达确立的他於1591年出版了分析方法入门,对代数学加以系统的整理,第一次自觉地使用字母来表示未知数和已知数韦达在他的另一部著作论方程的识别与订正中,改进了三四次方程的解法,还建立了二次和三次方程方程根与系数之间的关。
4、邦贝利在他的著作中阐述了三次方程不可约的情形,并使用了虚数,还改进了当时流行的代数符号符号代数学是由 一陆 世纪的法国数学家韦达确立的他於 一59一 年出版了分析方法入门,对代数学加以系统的整理,第一次自觉地使用字母来表示未知数和已知数韦达在他的另一部著作论方程的识别与订正中,改进了三;卡尔达诺被誉为百科全书式的人物,著作丰富,约有200多种文章和书籍,现存材料达7000页他的数学贡献主要体现在算术实践与个体测量1539和论掷骰游戏1663等作品中,展示了高超的计算技巧和概率论基础尤其是大术1545中,他首次公布了三四次代数方程的一般解法,引入了虚数;意思是活在当世就要好好享受人间的欢乐出自现代王蒙翻译的波斯诗人奥玛·海亚姆的鲁拜集原文无事需寻欢,有生莫断肠遣怀书共酒,何问寿与殇译文空闲的时候就要懂得享乐,有生之年不要愁断心肠抒发情怀,奋笔疾书,举杯共饮还提什么生老病死的;邦贝利在他的著作中阐述了三次方程不可约的情形,并使用了虚数,还改进了当时流行的代数符号符号代数学是由 16 世纪的法国数学家韦达确立的他於 1591 年出版了分析方法入门,对代数学加以系统的整理,第一次自觉地使用字母来表示未知数和已知数韦达在他的另一部著作论方程的识别与订正中,改进了三四次。